|
La pression est une
force appliquée sur une surface. Par exemple, chaque
cm2 (surface) de notre peau supporte
environ 1 kg (force) représentant le poids de
l'atmosphère. C'est la pression atmosphérique au
niveau de la mer. Nous ne la ressentons pas car
notre corps est incompressible et ses cavités
(estomac, poumons, sinus,... ) contiennent de l'air
à la même pression.
Si on s'élève de
5 000 m, la pression atmosphérique est deux fois
plus faible qu'au niveau de la mer car la masse
d'air au-dessus de notre tête est alors moitié
moindre. A la fin de cette page se trouve un tableau
des unités de pression. En plongée sous-marine, pour
mesurer la pression dans les problèmes, on utilise
de préférence le bar et on considère que
1 bar = 1 kg / cm2.
Qu'en est-il dans
l'eau ? Plus on est loin de la surface, plus la
pression est élevée car il faut tenir compte du
poids de l'eau au-dessus de nous. A -10 mètres de
profondeur, chaque cm2 de notre peau
supportera le poids d'un litre d'eau
(1 litre = 1 000 cm3). Sachant qu'un
litre d'eau pèse environ 1 kg, la pression
due à l'eau à -10 m de profondeur est donc
de 1 kg / cm2, c'est-à-dire 1 bar. Si on
descend à nouveau de -10 m, la pression augmentera à
nouveau de 1 bar.
La
pression absolue en
plongée est la pression totale : Pression
atmosphérique + Pression due à l'eau. A -10 m de
profondeur, la pression absolue est de 2 bar (1 bar
de pression atmosphérique + 1 bar du au poids de
10 m d'eau). A -20 m elle sera de 3 bar, à -30 m de
4 bar, etc... On remarquera que de 0 à -10 m la
pression augmente de 100% alors que si on descend de
-30 à -40 m, elle ne varie que de 20%. Il est
important de savoir que la pression varie plus vite
en fonction de la profondeur si on est près de la
surface.
La
pression hydrostatique est le nom savant
pour la pression due à l'eau. On l'appelle aussi
pression relative car c'est une
pression par rapport à la surface. La relation qui
unit tous ces termes est donc :
|
P.absolue = P.atmosphérique + P.hydrostatique
|
Mesure de la
pression :
Voici des précisions sur les unités utilisées pour
mesurer la pression. Dans les bouquins d'exercices
et de problèmes, on aime donner la pression en "cm
de mercure" (cm Hg). Cette vieille unité date d'une
expérience célèbre décrite par ce dessin :
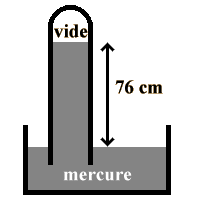 |
Toriccelli a retourné une éprouvette pleine
de mercure (métal liquide très lourd) dans
une cuve de mercure. Un vide s'est alors
créé en haut de l'éprouvette. En faisant
varier la position de l'éprouvette, il
constata que la distance entre la surface de
mercure au contact du vide et la surface de
mercure au contact de la pression
atmosphérique était constante et de 76 cm. |
Le poids de cette
colonne de 0,76 m de mercure équilibre parfaitement
la pression atmosphérique. Petit calcul : le mercure
pèse 13,6 g / cm3, cette colonne applique
donc une pression de 13,6 × 0,76 = 1,033 kg / cm2.
L'unité officielle
de pression dans le système international est le
pascal (Pa) qui est égal à une pression de 1 newton
par m2. Le bar, plus facile à utiliser
est un multiple du pascal : 1 bar = 100 000 Pa. Dans
les bulletins météo, on entend souvent parler de
l'hectopascal, qui est le nouveau nom du millibar.
La densité de
l'eau douce est 1, c'est-à-dire qu'un litre d'eau
douce pèse 1 kg. Pour faire l'expérience de
Torricelli avec de l'eau il aurait fallu utiliser
une éprouvette d'au moins 10,33 m ! Cette distance
est bien connue des installateurs de pompes
aspirantes : Une telle pompe ne peut pomper de l'eau
douce si elle est située à plus de 10,33 m de la
surface de la nappe. En effet, au delà de cette
distance elle ne pompe que de l'air et devient de ce
fait une "pompe à vide". Seule une pompe refoulante
placée au niveau de l'eau peut élever celle-ci
au-delà de 10,33 m.
L'eau de mer a une
densité de 1,026 à cause du sel qu'elle contient.
Pour tous les exercices on admettra que la pression
hydrostatique augmente de 1 bar tous les 10 m. En
réalité elle augmente de 0,98 bar dans l'eau douce
et de 1,007 bar dans l'eau de mer. Voici le calcul
pour l'eau de mer :
- Masse d'une
colonne d'eau de mer de 10 m de haut et 1 cm2
de section :
- 1,026 kg
- Poids de
cette colonne :
-
p = 1,026 × 9,81 = 10,06506 N (pour la suite, on
arrondi à 10,07)
- Pression
résultante :
-
P = 10,07 / 10-4 Pa = 100700 Pa = 1,007 bar
On remarque que
cette approximation va dans le sens de la sécurité
pour l'eau de mer, pas pour l'eau douce !
|
